Tutorial BYOL: Aprendizagem auto-supervisionada em imagens Cifar com código em Pytorch

Depois de apresentar Simclra Contrastiva Estrutura de aprendizagem auto-supervisionada, decidi demonstrar outro método infame, chamado BYOL. Bootstrap seu próprio latente (BYOL), é um novo algoritmo para aprendizado auto-supervisionado de representações de imagem. BYOL tem duas vantagens principais:

Não usa explicitamente amostras negativas. Em vez disso, minimiza diretamente a semelhança de representações da mesma imagem sob uma visão aumentada diferente (par positivo). Amostras negativas são imagens do lote diferente do par positivo.
Como resultado, BYOL Alega -se que exige tamanhos menores de lote, o que o torna uma escolha atraente.

Abaixo, você pode examinar o método. Ao contrário do artigo original, chamo o aluno da rede on -line e o professor de rede -alvo.

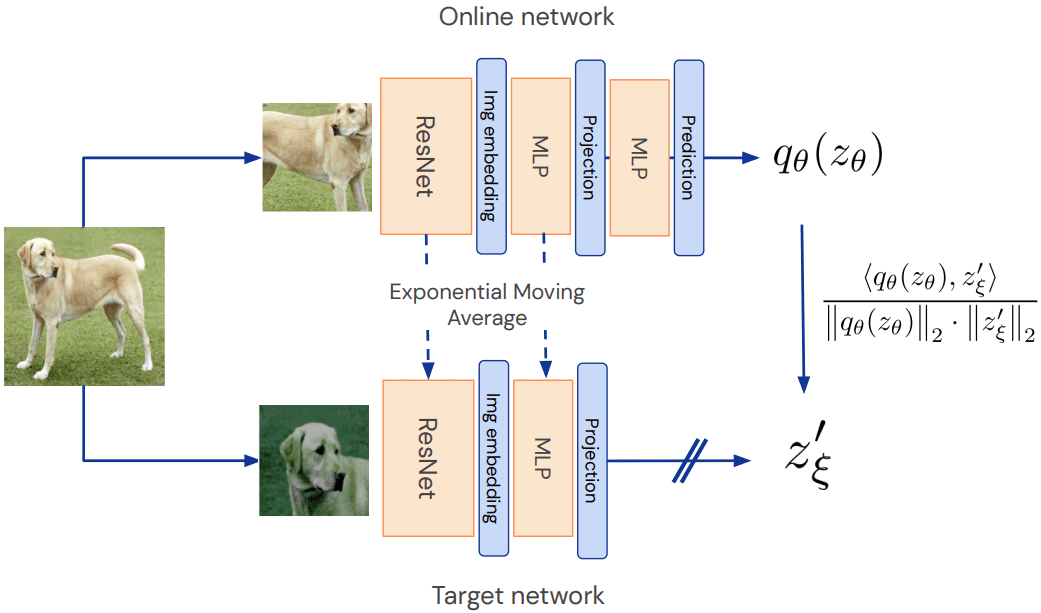
Visão geral do método BYOL. Fonte: BYOL Paper

Rede on -line aka aluno: comparado ao SIMCLR, há um segundo MLP, chamado preditoro que torna todo o método assimétrico. Assimétrico em comparação com o quê? Bem, para o modelo do professor (rede de destino).

Por que isso é importante?

Porque o modelo do professor é atualizado apenas Através da média móvel exponencial (EMA) dos parâmetros do aluno. Por fim, a cada iteração, uma pequena porcentagem (menos de 1%) dos parâmetros do aluno é passada ao professor. Por isso, Gradientes fluem apenas através da rede de estudantes. Isso pode ser implementado como:

class EMA():
   def __init__(self, alpha):
       super().__init__()
       self.alpha = alpha
   def update_average(self, old, new):
       if old is None:
           return new
       return old * self.alpha + (1 - self.alpha) * new
ema = EMA(0.99)
for student_params, teacher_params in zip(student_model.parameters(),teacher_model.parameters()):
         old_weight, up_weight = teacher_params.data, student_params.data
         teacher_params.data = ema.update_average(old_weight, up_weight)

Outra diferença importante entre Simclr e BYOL é a função de perda.

Função de perda

O MLP preditor é apenas aplicado ao aluno, fazendo a arquitetura assimétrico. Esta é uma opção de design -chave para evitar o colapso do modo. Colapso do modo Aqui seria produzir a mesma projeção para todas as entradas.

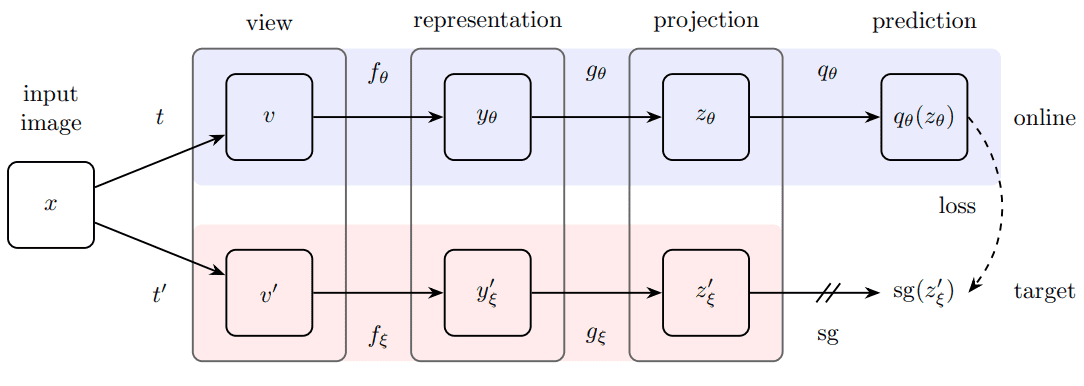
Visão geral do método BYOL. Fonte: BYOL Paper

Finalmente, os autores definiram o seguinte erro médio ao quadrado entre as previsões normalizadas de L2 e as projeções de destino:

\ mathcal {l} _ {\ theta, \ xi} \triangleq\left\|\bar{q}_{\theta}\left(z_{\theta}\right)-\bar{z}_{\xi}^{\prime}\right\|_{2}^{2}=2-2 \cdot \frac{\left\langle q _ {\ theta} \ esquerda (z _ {\ theta} \ direita), z _ {\ xi}^{\ prime} \ right \ rangle} {\ \ \ | \ cdot \ esquerda \ | z _ {\ xi}^{\ prime} \ direita \ | _ {2}}.

A perda de L2 pode ser implementada da seguinte maneira. L2 Normalização é aplicado de antemão.

import torch
import torch.nn.functional as F
def loss_fn(x, y):
   x = F.normalize(x, dim=-1, p=2)
   y = F.normalize(y, dim=-1, p=2)
   return 2 - 2 * (x * y).sum(dim=-1)

O código está disponível em Girub

Rastreando o que está acontecendo em pré-treinamento auto-supervisionado: precisão de knn

No entanto, a perda de aprendizado auto-supervisionada não é uma métrica confiável para rastrear. O que eu descobri ser a melhor maneira de rastrear o que está acontecendo durante o treinamento é medir a precisão da κν.

A vantagem crítica de usar o KNN é que não precisamos treinar um classificador linear em cima a cada vez, para que seja mais rápido e completamente sem supervisão.

Nota: A medição do KNN se aplica apenas à classificação da imagem, mas você obtém a ideia. Para esse fim, fiz uma aula para encapsular a lógica do KNN em nosso contexto:

import numpy as np
import torch
from sklearn.model_selection import cross_val_score
from sklearn.neighbors import KNeighborsClassifier
from torch import nn
class KNN():
   def __init__(self, model, k, device):
       super(KNN, self).__init__()
       self.k = k
       self.device = device
       self.model = model.to(device)
       self.model.eval()
   def extract_features(self, loader):
       """
       Infer/Extract features from a trained model
       Args:
           loader: train or test loader
       Returns: 3 tensors of all:  input_images, features, labels
       """
       x_lst = ()
       features = ()
       label_lst = ()
       with torch.no_grad():
           for input_tensor, label in loader:
               h = self.model(input_tensor.to(self.device))
               features.append(h)
               x_lst.append(input_tensor)
               label_lst.append(label)
           x_total = torch.stack(x_lst)
           h_total = torch.stack(features)
           label_total = torch.stack(label_lst)
           return x_total, h_total, label_total
   def knn(self, features, labels, k=1):
       """
       Evaluating knn accuracy in feature space.
       Calculates only top-1 accuracy (returns 0 for top-5)
       Args:
           features: (... , dataset_size, feat_dim)
           labels: (... , dataset_size)
           k: nearest neighbours
       Returns: train accuracy, or train and test acc
       """
       feature_dim = features.shape(-1)
       with torch.no_grad():
           features_np = features.cpu().view(-1, feature_dim).numpy()
           labels_np = labels.cpu().view(-1).numpy()
           self.cls = KNeighborsClassifier(k, metric="cosine").fit(features_np, labels_np)
           acc = self.eval(features, labels)
       return acc
   def eval(self, features, labels):
     feature_dim = features.shape(-1)
     features = features.cpu().view(-1, feature_dim).numpy()
     labels = labels.cpu().view(-1).numpy()
     acc = 100 * np.mean(cross_val_score(self.cls, features, labels))
     return acc
   def _find_best_indices(self, h_query, h_ref):
       h_query = h_query / h_query.norm(dim=1).view(-1, 1)
       h_ref = h_ref / h_ref.norm(dim=1).view(-1, 1)
       scores = torch.matmul(h_query, h_ref.t())  
       score, indices = scores.topk(1, dim=1)  
       return score, indices
   def fit(self, train_loader, test_loader=None):
       with torch.no_grad():
           x_train, h_train, l_train = self.extract_features(train_loader)
           train_acc = self.knn(h_train, l_train, k=self.k)
           if test_loader is not None:
               x_test, h_test, l_test = self.extract_features(test_loader)
               test_acc = self.eval(h_test, l_test)
               return train_acc, test_acc

Agora podemos nos concentrar no método e no modelo BYOL.

Modificar resnet: Adicionar cabeças de projeção MLP

Começaremos com um modelo básico (Resnet18) e modificamos-o para o aprendizado auto-supervisionado. A última camada que normalmente faz a classificação é substituída por uma função de identidade. Os recursos de saída do RESNET18 serão alimentados ao projetor MLP.

import copy
import torch
from torch import nn
import torch.nn.functional as F
class MLP(nn.Module):
   def __init__(self, dim, embedding_size=256, hidden_size=2048, batch_norm_mlp=False):
       super().__init__()
       norm = nn.BatchNorm1d(hidden_size) if batch_norm_mlp else nn.Identity()
       self.net = nn.Sequential(
           nn.Linear(dim, hidden_size),
           norm,
           nn.ReLU(inplace=True),
           nn.Linear(hidden_size, embedding_size)
       )
   def forward(self, x):
       return self.net(x)
class AddProjHead(nn.Module):
   def __init__(self, model, in_features, layer_name, hidden_size=4096,
                embedding_size=256, batch_norm_mlp=True):
       super(AddProjHead, self).__init__()
       self.backbone = model
       setattr(self.backbone, layer_name, nn.Identity())
       self.backbone.conv1 = torch.nn.Conv2d(3, 64, kernel_size=3, stride=1, padding=1, bias=False)
       self.backbone.maxpool = torch.nn.Identity()
       self.projection = MLP(in_features, embedding_size, hidden_size=hidden_size, batch_norm_mlp=batch_norm_mlp)
   def forward(self, x, return_embedding=False):
       embedding = self.backbone(x)
       if return_embedding:
           return embedding
       return self.projection(embedding)

Também substituí a primeira camada de convúria do Resnet18 da convolução 7×7 a 3×3, pois estamos tocando com imagens 32×32 (CIFAR-10).

O código está disponível em Girub. Se você planeja solidificar seu conhecimento pytorch, há dois livros incríveis que recomendamos: Aprendizado profundo com pytorch das publicações de Manning e Aprendizado de máquina com Pytorch e Scikit-Learn Por Sebastian Raschka. Você sempre pode usar o código de desconto de 35% Blaisummer21 Para todos os produtos de Manning.

O método BYOL real

Até agora, apresentei todos os componentes importantes para chegar a esse ponto. Agora vamos construir o BYOL Módulo com nossas amadas redes de alunos e professores. Observe que o MLP e o projetor preditores do aluno são idênticos.

Minha implementação do BYOL foi baseada em lucidrains ‘ repo. Eu o modifiquei para torná -lo mais simples e brincar com ele.

class BYOL(nn.Module):
   def __init__(
           self,
           net,
           batch_norm_mlp=True,
           layer_name='fc',
           in_features=512,
           projection_size=256,
           projection_hidden_size=2048,
           moving_average_decay=0.99,
           use_momentum=True):
       """
       Args:
           net: model to be trained
           batch_norm_mlp: whether to use batchnorm1d in the mlp predictor and projector
           in_features: the number features that are produced by the backbone net i.e. resnet
           projection_size: the size of the output vector of the two identical MLPs
           projection_hidden_size: the size of the hidden vector of the two identical MLPs
           augment_fn2: apply different augmentation the second view
           moving_average_decay: t hyperparameter to control the influence in the target network weight update
           use_momentum: whether to update the target network
       """
       super().__init__()
       self.net = net
       self.student_model = AddProjHead(model=net, in_features=in_features,
                                        layer_name=layer_name,
                                        embedding_size=projection_size,
                                        hidden_size=projection_hidden_size,
                                        batch_norm_mlp=batch_norm_mlp)
       self.use_momentum = use_momentum
       self.teacher_model = self._get_teacher()
       self.target_ema_updater = EMA(moving_average_decay)
       self.student_predictor = MLP(projection_size, projection_size, projection_hidden_size)
   @torch.no_grad()
   def _get_teacher(self):
       return copy.deepcopy(self.student_model)
   @torch.no_grad()
   def update_moving_average(self):
       assert self.use_momentum, 'you do not need to update the moving average, since you have turned off momentum ' \
                                 'for the target encoder '
       assert self.teacher_model is not None, 'target encoder has not been created yet'
       for student_params, teacher_params in zip(self.student_model.parameters(), self.teacher_model.parameters()):
         old_weight, up_weight = teacher_params.data, student_params.data
         teacher_params.data = self.target_ema_updater.update_average(old_weight, up_weight)
   def forward(
           self,
           image_one, image_two=None,
           return_embedding=False):
       if return_embedding or (image_two is None):
           return self.student_model(image_one, return_embedding=True)
       student_proj_one = self.student_model(image_one)
       student_proj_two = self.student_model(image_two)
       student_pred_one = self.student_predictor(student_proj_one)
       student_pred_two = self.student_predictor(student_proj_two)
       with torch.no_grad():
           teacher_proj_one = self.teacher_model(image_one).detach_()
           teacher_proj_two = self.teacher_model(image_two).detach_()
       loss_one = loss_fn(student_pred_one, teacher_proj_one)
       loss_two = loss_fn(student_pred_two, teacher_proj_two)       
       return (loss_one + loss_two).mean()

Para o CIFAR-10, basta usar o 2048 como uma dimensão oculta e 256 como a dimensão de incorporação. Treinaremos um resnet18 que gera 512 recursos para 100 épocas. As partes do código que se referem ao carregamento e aumento de dados são omitidas para aumentar a legibilidade. Você pode procurá -los no código.

Você pode usar o Adam Optimizer ( $lr = 3 * 10^{-4}$

A única coisa que será alterada no código do trem é a atualização da EMA.

def training_step(model, data):
   (view1, view2), _ = data
   loss = model(view1.cuda(), view2.cuda())
   return loss
def train_one_epoch(model, train_dataloader, optimizer):
   model.train()
   total_loss = 0.
   num_batches = len(train_dataloader)
   for data in train_dataloader:
       optimizer.zero_grad()
       loss = training_step(model, data)
       loss.backward()
       optimizer.step()
       model.update_moving_average()
       total_loss += loss.item()
   return total_loss/num_batches

Vamos pular nos resultados!

Resultados: Precisão de KNN vs épocas de pré -treinamento

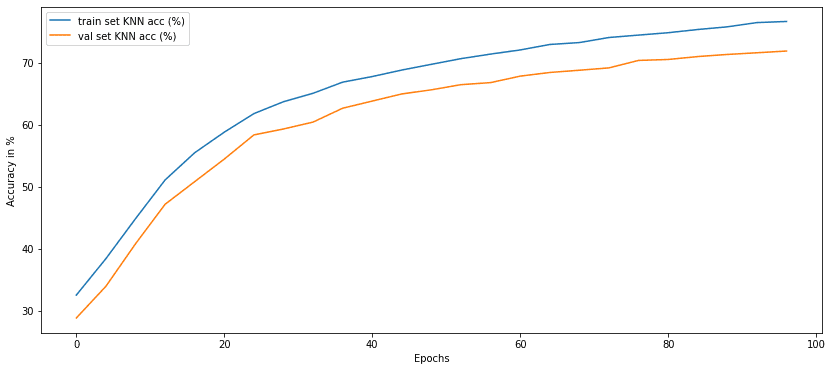
Precisão de knn a cada 4 épocas. Imagem por autor

Não é incrível que, sem rótulos, possamos atingir uma precisão de validação de 70%? Achei isso incrível, especialmente para esse método que parece ser menos sensível ao tamanho do lote.

Mas por que o tamanho do lote tem um efeito aqui? Não deveria estar usando Paris negativo? De onde vem a dependência do tamanho do lote?

Resposta curta: Bem, é a normalização do lote nas camadas do MLP!

Aqui estão os experimentos que fiz para cruzá-lo.

Uma nota sobre norma em lote em redes MLP e Momentum EMA

Fiquei curioso para observar o colapso do modo sem normalização do lote. Você pode tentar isso sozinho configurando:

model = BYOL(model, in_features=512, batch_norm_mlp=False)

Eu observei que a distância L2 vai quase zero das primeiras épocas:

Epoch 0: loss:0.06423207696957084

Epoch 8: loss:0.005584242034894534

Epoch 20: loss:0.005460431350347323

A perda vai para aproximadamente zero e o KNN para de aumentar (35% vs 60% na configuração normal). É por isso que afirma que BYOL implicitamente Usa uma forma de aprendizado contrastante, alavancando as estatísticas do lote nos MLPs. Aqui está a precisão do KNN:

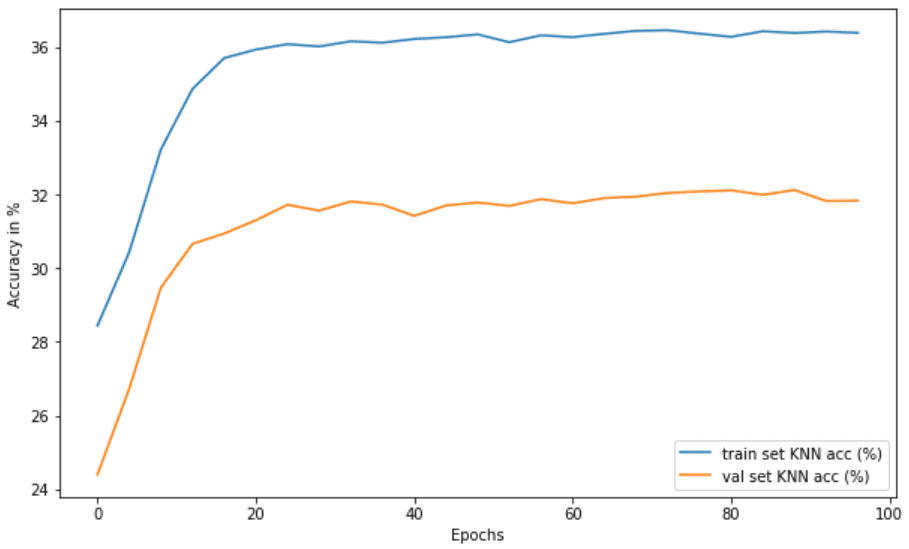
O colapso do modo no BYOL removendo a norma em lote nos MLPs. Imagem por autor

Estou bem ciente dos trabalhos que mostram que as estatísticas em lote não são a única condição para o BYOL funcionar. Este é um post experimental, então não vou jogar esse jogo. Eu estava curioso para observar o colapso do modo aqui.

Conclusão

Para uma explicação mais detalhada do método, verifique o vídeo de Yannic no BYOL:

https://www.youtube.com/watch?v=ypfuiomyoee

Neste tutorial, implementamos o BYOL passo a passo e pré -criados no CIFAR10. Observamos o aumento maciço da precisão do KNN, combinando as representações da mesma imagem. Um classificador aleatório teria 10% e, com 100 épocas, atingimos uma precisão de validação de KNN de 70% sem rótulos. Quão legal é isso?

Para saber mais sobre aprendizado auto-supervisionadofique atento! Apoie -nos pelo compartilhamento de mídia social, fazendo um doaçãoou comprar nosso aprendizado profundo em produção livro. Seria muito apreciado.

* Divulgação: Observe que alguns dos links acima podem ser links de afiliados e, sem nenhum custo adicional, ganharemos uma comissão se você decidir fazer uma compra depois de clicar.