Quando percebi que não posso aplicar pipelines comuns de processamento de imagens em imagens médicas, fiquei completamente desencorajado. Por que essa funcionalidade não existe? Então, eu inventei este post (mais um caderno) para indivíduos desencorajados que, como eu, estão interessados em resolver problemas de imagem médica.
Já discutimos a segmentação de imagem médica e alguns antecedentes iniciais em Sistemas de coordenadas e arquivos dicom. Minha experiência no campo me leva a continuar com o entendimento dos dados, o pré -processamento e alguns aumentos. Como eu sempre digo, se você apenas entende seus dados e suas particularidades, provavelmente está jogando bingo. No campo da imagem médica, encontro algumas manipulações de dados, que são fortemente usadas no pré-processamento e aumento nos métodos de última geração, para serem críticos em nosso entendimento. Para esse fim, eu forneço um caderno para todos brincarem. Ele realiza transformações em imagens médicas, que são simplesmente uma grade estruturada em 3D.
Para se aprofundar na maneira como a IA é usada na medicina, você não pode errar com o Você tem para medicina Curso on -line, oferecido pela Coursera. Se você deseja se concentrar na análise de imagem médica com aprendizado profundo, eu recomendo começar a partir do Curso de Udemy, baseado em Pytorch.
Dados: Tocaremos com 2 imagens de ressonância magnética fornecidas pela Nibabel (Biblioteca Python) para fins de ilustração. As imagens são armazenadas como arquivos bacanas. Mas antes disso, vamos escrever algum código para visualizar os volumes médicos 3D.
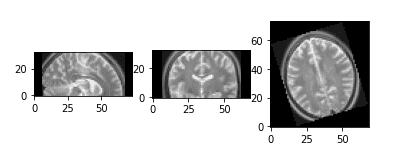
As imagens serão mostradas em 3 aviões: sagital, coronal e axial da esquerda para a direita durante todo o post.
Visualização de planos bidimensionais
Em todo o tutorial, usaremos extensivamente uma função que visualiza as três fatias medianas no sagital, coronal e axial aviões respectivamente. Vamos escrever uma função mínima para fazê -lo:
def show_mid_slice(img_numpy, title='img'):
"""
Accepts an 3D numpy array and shows median slices in all three planes
"""
assert img_numpy.ndim == 3
n_i, n_j, n_k = img_numpy.shape
center_i1 = int((n_i - 1) / 2)
center_j1 = int((n_j - 1) / 2)
center_k1 = int((n_k - 1) / 2)
show_slices((img_numpy(center_i1, :, :),
img_numpy(:, center_j1, :),
img_numpy(:, :, center_k1)))
plt.suptitle(title)
def show_slices(slices):
"""
Function to display a row of image slices
Input is a list of numpy 2D image slices
"""
fig, axes = plt.subplots(1, len(slices))
for i, slice in enumerate(slices):
axes(i).imshow(slice.T, cmap="gray", origin="lower")
Nada mais do que o matplotlib “imshow" e manipulações de matriz de Numpy. Para o registro, as imagens médicas são um único canal e as visualizamos em cores em escala de cinza.
As duas imagens que usaremos para brincar com uma infinidade de transformações podem ser ilustradas abaixo:
show_mid_slice(epi_img_numpy, 'first image')
show_mid_slice(anatomy_img_numpy,'second image')
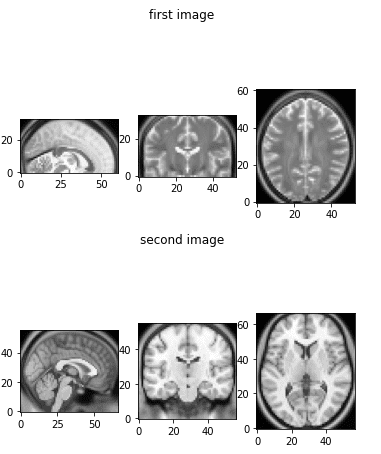
As imagens iniciais de ressonância magnética do cérebro que usaremos.
Agora estamos prontos para ir! Vamos começar com redimensionar e redimensionar imagens médicas. Sim, não é exatamente o mesmo.
Redimensionamento da imagem médica (para baixo/amostragem)
O Scipy A biblioteca fornece muitas funcionalidades para imagens multidimensionais. Como as imagens médicas são tridimensionais, muitas funcionalidades podem ser usadas. Desta vez vamos usar Scipy.nowage.tinepoinntion.zoom para redimensionar a imagem nas dimensões desejadas. Isso é semelhante à amostragem em uma imagem 2D. A mesma função pode ser usada para interpolação para aumentar as dimensões espaciais. Como ilustração, dobraremos e metade do tamanho da imagem original.
Lembre -se de que, nesse tipo de transformação, as proporções geralmente são importantes a serem mantidas.
Você provavelmente não quer perder a anatomia do corpo humano 🙂
import scipy
def resize_data_volume_by_scale(data, scale):
"""
Resize the data based on the provided scale
"""
scale_list = (scale,scale,scale)
return scipy.ndimage.interpolation.zoom(data, scale_list, order=0)
result = resize_data_volume_by_scale(epi_img_numpy, 0.5)
result2 = resize_data_volume_by_scale(epi_img_numpy, 2)
Esse tipo de escala é geralmente chamado de isométrica. Honestamente, eu não sou um grande fã da terminologia da Scipy para usar a palavra zoom para essa funcionalidade.
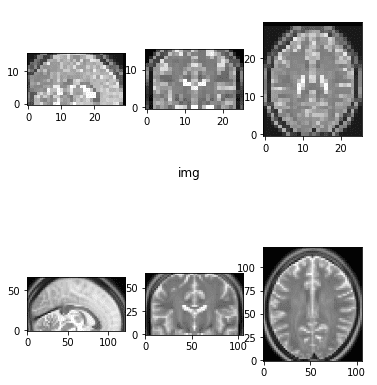
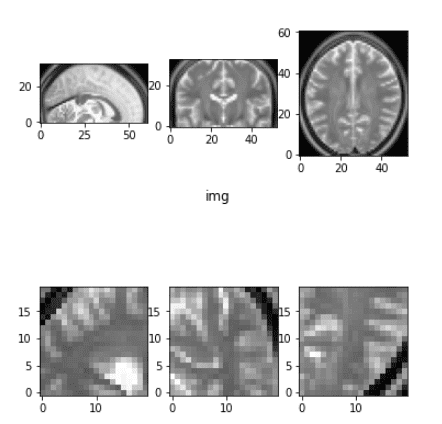
Desmembrou a imagem e ascensão por um fator de 2
É muito comum reduzir a imagem em uma dimensão mais baixa para o aprendizado de máquina pesado.
Observe que há outro tipo de redimensionamento. Em vez de fornecer a forma de saída desejada, você especifica o tamanho da voxel desejado (por exemplo, voxel_size = (1,1,1) mm). Nibabel fornece uma função chamada reample_to_output (). Funciona com arquivos nifti e não com matrizes Numpy. Honestamente, eu não recomendaria sozinho, pois as imagens resultantes podem não ter a mesma forma. Isso pode ser um problema para o aprendizado profundo. Por exemplo, para criar lotes com Dataloaders, a dimensão deve ser consistente nas instâncias. No entanto, você pode optar por incluí -lo em uma etapa anterior em seu pipeline. Pode ser usado para trazer imagens diferentes para ter o mesmo tamanho de voxel ou similar.
Redaling de imagem médica (zoom-in/out)
O redimensionamento pode ser considerado como uma transformação afim. Vamos dar um zoom aleatoriamente dentro e fora da imagem. Esse aumento geralmente ajuda o modelo a aprender recursos invariantes em escala.
def random_zoom(matrix,min_percentage=0.7, max_percentage=1.2):
z = np.random.sample() *(max_percentage-min_percentage) + min_percentage
zoom_matrix = np.array(((z, 0, 0, 0),
(0, z, 0, 0),
(0, 0, z, 0),
(0, 0, 0, 1)))
return ndimage.interpolation.affine_transform(matrix, zoom_matrix)
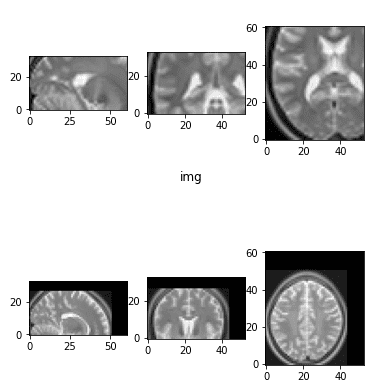
Zoom aleatório e amplie o zoom
É importante ver que a área vazia está preenchida com pixels pretos (intensidade zero).
Observe aqui que o ar circundante em imagens médicas não tem intensidade zero. O preto é realmente relativo às imagens médicas.
O próximo na lista é a rotação 3D.
Rotação de imagem médica
A rotação é um dos métodos mais comuns para obter aumento de dados na visão computacional. Também tem sido considerado uma técnica auto-supervisionada com resultados notáveis (Spyros Gidaris et al. ).
Na imagem médica, é uma funcionalidade de importação igual que também tem sido usada de pré-treinamento auto-supervisionado (Xinrui Zhuang et al. 2019 ). Uma rotação 3D aleatória simples em uma determinada gama de graus pode ser ilustrada com o código abaixo:
def random_rotate3D(img_numpy, min_angle, max_angle):
"""
Returns a random rotated array in the same shape
:param img_numpy: 3D numpy array
:param min_angle: in degrees
:param max_angle: in degrees
"""
assert img_numpy.ndim == 3, "provide a 3d numpy array"
assert min_angle < max_angle, "min should be less than max val"
assert min_angle > -360 or max_angle < 360
all_axes = ((1, 0), (1, 2), (0, 2))
angle = np.random.randint(low=min_angle, high=max_angle+1)
axes_random_id = np.random.randint(low=0, high=len(all_axes))
axes = all_axes(axes_random_id)
return scipy.ndimage.rotate(img_numpy, angle, axes=axes)
Simplesmente temos que definir o eixo e o ângulo de rotação. Como a escala proporcionou ao modelo mais diversidade, a fim de aprender características invariantes em escala, a rotação auxilia no aprendizado de recursos invariantes à rotação.
O próximo em nossa lista é o lançamento da imagem.
Flip de imagem médica
Semelhante às imagens RGB comuns, podemos executar o eixo lançando imagens médicas. Neste ponto, é realmente importante esclarecer uma coisa:
Quando realizamos aumentos e/ou pré -processamento em nossos dados, podemos ter que aplicar operações semelhantes nos dados da verdade no solo.
Por exemplo, se resolvermos a tarefa de Segmentação de imagem médicaé importante virar o mapa de segmentação de destino. Uma implementação simples pode ser encontrada abaixo:
def random_flip(img, label=None):
axes = (0, 1, 2)
rand = np.random.randint(0, 3)
img = flip_axis(img, axes(rand))
img = np.squeeze(img)
if label is None:
return img
else:
y = flip_axis(y, axes(rand))
y = np.squeeze(y)
return x, y
def flip_axis(x, axis):
x = np.asarray(x).swapaxes(axis, 0)
x = x(::-1, ...)
x = x.swapaxes(0, axis)
return x
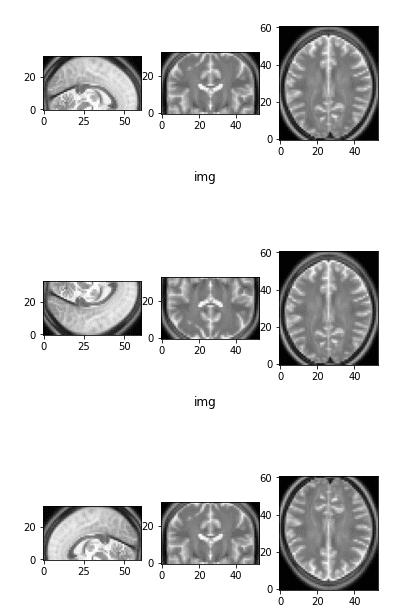
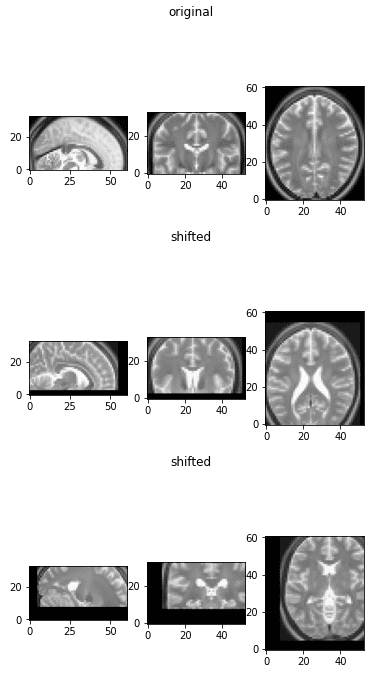
A imagem inicial como referência e duas versões invertidas
Observe que, lançando um eixo, duas visualizações mudam. A primeira imagem na parte superior é a imagem inicial como referência.
Mudança de imagem médica (deslocamento)
Aqui eu gostaria de dizer outra coisa.
Rotação, mudança e escala não passam de transformações afins.
Às vezes, eu os implemento apenas definindo as transformações afins e aplico na imagem com o Scipy, e às vezes uso as funções já implementadas para o processamento de imagem multidimensional.
Para usar esta operação no meu pipeline de aumento de dados, você pode ver que incluí uma função de wrapper. Este último basicamente amostra um número aleatório, geralmente na faixa desejada, e chama a função de transformação afim. Abaixo está a implementação para mudança/deslocamento aleatório.
def transform_matrix_offset_center_3d(matrix, x, y, z):
offset_matrix = np.array(((1, 0, 0, x), (0, 1, 0, y), (0, 0, 1, z), (0, 0, 0, 1)))
return ndimage.interpolation.affine_transform(matrix, offset_matrix)
def random_shift(img_numpy, max_percentage=0.4):
dim1, dim2, dim3 = img_numpy.shape
m1,m2,m3 = int(dim1*max_percentage/2),int(dim1*max_percentage/2), int(dim1*max_percentage/2)
d1 = np.random.randint(-m1,m1)
d2 = np.random.randint(-m2,m2)
d3 = np.random.randint(-m3,m3)
return transform_matrix_offset_center_3d(img_numpy, d1, d2, d3)
Esse aumento não é muito comum no aumento da imagem médica, mas os incluímos aqui para completar.
A razão pela qual não incluímos é que as redes neurais convolucionais são, por definição, projetadas para aprender recursos invariantes à tradução.
Cultura 3D aleatória
O corte também não é significativamente diferente das imagens naturais. No entanto, lembre -se de que geralmente precisamos levar todas as fatias de uma dimensão e precisamos cuidar disso. O motivo é que uma dimensão pode ter menos fatias que as outras. Por exemplo, uma vez eu tive que lidar com uma imagem de 384x384x64, que é comum em Imagens de CT.
def crop_3d_volume(img_tensor, crop_dim, crop_size):
assert img_tensor.ndim == 3, '3d tensor must be provided'
full_dim1, full_dim2, full_dim3 = img_tensor.shape
slices_crop, w_crop, h_crop = crop_dim
dim1, dim2, dim3 = crop_size
if full_dim1 == dim1:
img_tensor = img_tensor(:, w_crop:w_crop + dim2,
h_crop:h_crop + dim3)
elif full_dim2 == dim2:
img_tensor = img_tensor(slices_crop:slices_crop + dim1, :,
h_crop:h_crop + dim3)
elif full_dim3 == dim3:
img_tensor = img_tensor(slices_crop:slices_crop + dim1, w_crop:w_crop + dim2, :)
else:
img_tensor = img_tensor(slices_crop:slices_crop + dim1, w_crop:w_crop + dim2,
h_crop:h_crop + dim3)
return img_tensor
def find_random_crop_dim(full_vol_dim, crop_size):
assert full_vol_dim(0) >= crop_size(0), "crop size is too big"
assert full_vol_dim(1) >= crop_size(1), "crop size is too big"
assert full_vol_dim(2) >= crop_size(2), "crop size is too big"
if full_vol_dim(0) == crop_size(0):
slices = crop_size(0)
else:
slices = np.random.randint(full_vol_dim(0) - crop_size(0))
if full_vol_dim(1) == crop_size(1):
w_crop = crop_size(1)
else:
w_crop = np.random.randint(full_vol_dim(1) - crop_size(1))
if full_vol_dim(2) == crop_size(2):
h_crop = crop_size(2)
else:
h_crop = np.random.randint(full_vol_dim(2) - crop_size(2))
return (slices, w_crop, h_crop)
Existem outras técnicas para o corte que se concentram na área em que estamos interessados, ou seja, o tumor, mas não entraremos nisso agora.
Até agora, brincamos com transformações geométricas. Vamos ver o que podemos fazer com a intensidade da imagem.
Valores de intensidade do clipe (outliers)
Esta etapa não é aplicável a este tutorial, mas pode ser bastante útil em geral. Especialmente para Imagens de CT. A razão pela qual não é aplicável é que as imagens de ressonância magnética estão em uma gama bastante estreita de valores.
def percentile_clip(img_numpy, min_val=5, max_val=95):
"""
Intensity normalization based on percentile
Clips the range based on the quartile values.
:param min_val: should be in the range (0,100)
:param max_val: should be in the range (0,100)
:return: intensity normalized image
"""
low = np.percentile(img_numpy, min_val)
high = np.percentile(img_numpy, max_val)
img_numpy(img_numpy < low) = low
img_numpy(img_numpy > high) = high
return img_numpy
def clip_range(img_numpy, min_intensity=10, max_intensity=240):
return np.clip(img_numpy, min_intensity, max_intensity)
Normalização de intensidade em imagens médicas
Aqui, incluo as normalizações de intensidade mais comuns: min-max e média/std. Uma coisinha a ter em mente:
Quando realizamos normalização média/padrão, geralmente omitimos os voxels de intensidade zero a partir do cálculo da média. Isso vale principalmente para imagens de ressonância magnética.
Uma maneira de olhar para isso é se tivermos uma imagem cerebral; Provavelmente não queremos normalizá -lo com a intensidade dos voxels ao seu redor.
def normalize_intensity(img_tensor, normalization="mean"):
"""
Accepts an image tensor and normalizes it
:param normalization: choices = "max", "mean" , type=str
For mean normalization we use the non zero voxels only.
"""
if normalization == "mean":
mask = img_tensor.ne(0.0)
desired = img_tensor(mask)
mean_val, std_val = desired.mean(), desired.std()
img_tensor = (img_tensor - mean_val) / std_val
elif normalization == "max":
MAX, MIN = img_tensor.max(), img_tensor.min()
img_tensor = (img_tensor - MIN) / (MAX - MIN)
return img_tensor
Não faz sentido visualizar essa transformação, pois seu objetivo é alimentar os dados pré -processados no modelo de aprendizado profundo. Obviamente, qualquer outro tipo de normalização da intensidade pode ser aplicado em imagens médicas.
Deformação elástica
Quando li essa transformação pela primeira vez no artigo UNET original, não entendi uma única palavra do parágrafo:
“Quanto às nossas tarefas, existem muito poucos dados de treinamento disponíveis, usamos o aumento excessivo de dados aplicando deformações elásticas às imagens de treinamento disponíveis. Isso permite que a rede aprenda invariância a tais deformações, sem a necessidade de ver essas transformações na imagem mais comum no segmento de imagens mais importantes. Olaf Ronneberger et al. 2015 (sonhos de papel)
Honestamente, não analisei a publicação original de 2003. E você provavelmente também não. Eu olhei para outras implementações de código e tentei torná -lo mais simples. Decidi incluí -lo no meu tutorial porque você verá muito na literatura.
def elastic_transform_3d(image, labels=None, alpha=4, sigma=35, bg_val=0.1):
"""
Elastic deformation of images as described in
Simard, Steinkraus and Platt, "Best Practices for
Convolutional Neural Networks applied to Visual
Document Analysis", in
Proc. of the International Conference on Document Analysis and
Recognition, 2003.
Modified from:
https://gist.github.com/chsasank/4d8f68caf01f041a6453e67fb30f8f5a
https://github.com/fcalvet/image_tools/blob/master/image_augmentation.py#L62
Modified to take 3D inputs
Deforms both the image and corresponding label file
image linear/trilinear interpolated
Label volumes nearest neighbour interpolated
"""
assert image.ndim == 3
shape = image.shape
dtype = image.dtype
coords = np.arange(shape(0)), np.arange(shape(1)), np.arange(shape(2))
im_intrps = RegularGridInterpolator(coords, image,
method="linear",
bounds_error=False,
fill_value=bg_val)
dx = gaussian_filter((np.random.rand(*shape) * 2 - 1), sigma,
mode="constant", cval=0.) * alpha
dy = gaussian_filter((np.random.rand(*shape) * 2 - 1), sigma,
mode="constant", cval=0.) * alpha
dz = gaussian_filter((np.random.rand(*shape) * 2 - 1), sigma,
mode="constant", cval=0.) * alpha
x, y, z = np.mgrid(0:shape(0), 0:shape(1), 0:shape(2))
indices = np.reshape(x + dx, (-1, 1)), \
np.reshape(y + dy, (-1, 1)), \
np.reshape(z + dz, (-1, 1))
image = np.empty(shape=image.shape, dtype=dtype)
image = im_intrps(indices).reshape(shape)
if labels is not None:
lab_intrp = RegularGridInterpolator(coords, labels,
method="nearest",
bounds_error=False,
fill_value=0)
labels = lab_intrp(indices).reshape(shape).astype(labels.dtype)
return image, labels
return image
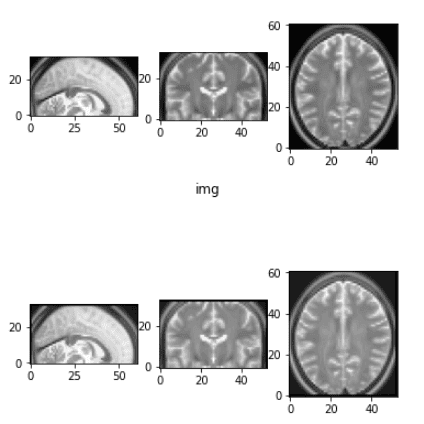
Antes e depois da deformação elástica
O que você precisa ter em mente é que essa transformação altera a intensidade e aplica algum ruído gaussiano em cada dimensão. Para mais informações, você deve voltar ao original trabalhar.
Conclusão
Até agora você pode ressoar com meus pensamentos sobre as particularidades sobre o pré -processamento e os aumentos de imagens médicas. Mas não se esqueça: você pode brincar com o tutorial online E veja as transformações sozinho. Ajuda, acredite em mim. Compreender nossas imagens médicas é importante. Agora você pode escolher quais transformações para aplicar em seu projeto.
Se você gostou do nosso tutorial, sinta -se à vontade para compartilhá -lo em sua página de mídia social, como uma recompensa pelo nosso trabalho. Seria muito apreciado.
Fique ligado para mais artigos de verão da IA!
* Divulgação: Observe que alguns dos links acima podem ser links de afiliados e, sem nenhum custo adicional, ganharemos uma comissão se você decidir fazer uma compra depois de clicar.